Introduction to zfit¶
In this notebook, we will have a walk through the main components of zfit and their features. Especially the extensive model building part will be discussed separately. zfit consists of 5 mostly independent parts. Other libraries can rely on this parts to do plotting or statistical inference, such as hepstats does. Therefore we will discuss two libraries in this tutorial: zfit to build models, data and a loss, minimize it and get a fit result and hepstats, to use the loss we built here and do inference.

Data¶
This component in general plays a minor role in zfit: it is mostly to provide a unified interface for data.
Preprocessing is therefore not part of zfit and should be done beforehand. Python offers many great possibilities to do so (e.g. Pandas).
zfit Data can load data from various sources, most notably from Numpy, Pandas DataFrame, TensorFlow Tensor and ROOT (using uproot). It is also possible, for convenience, to convert it directly to_pandas. The constructors are named from_numpy, from_root etc.
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
import zfit
from zfit import z
A Data needs not only the data itself but also the observables: the human readable string identifiers of the axes (corresponding to “columns” of a Pandas DataFrame). It is convenient to define the Space not only with the observable but also with a limit: this can directly be re-used as the normalization range in the PDF.
First, let’s define our observables
obs = zfit.Space('obs1', (-5, 10))
This Space has limits. Next to the effect of handling the observables, we can also play with the limits: multiple Spaces can be added to provide disconnected ranges. More importantly, Space offers functionality:
limit1d: return the lower and upper limit in the 1 dimensional case (raises an error otherwise)
rect_limits: return the n dimensional limits
area(): calculate the area (e.g. distance between upper and lower)
inside(): return a boolean Tensor corresponding to whether the value is inside the
Spacefilter(): filter the input values to only return the one inside
size_normal = 10000
data_normal_np = np.random.normal(size=size_normal, scale=2)
data_normal = zfit.Data.from_numpy(obs=obs, array=data_normal_np)
The main functionality is
nevents: attribute that returns the number of events in the object
data_range: a
Spacethat defines the limits of the data; if outside, the data will be cutn_obs: defines the number of dimensions in the dataset
with_obs: returns a subset of the dataset with only the given obs
weights: event based weights
Furthermore, value returns a Tensor with shape (nevents, n_obs).
To retrieve values, in general z.unstack_x(data) should be used; this returns a single Tensor with shape (nevents) or a list of tensors if n_obs is larger then 1.
print(f"We have {data_normal.nevents} events in our dataset with the minimum of {np.min(data_normal.unstack_x())}") # remember! The obs cut out some of the data
We have 9931 events in our dataset with the minimum of -4.994790077305963
data_normal.n_obs
1
Model¶
Building models is by far the largest part of zfit. We will therefore cover an essential part, the possibility to build custom models, in an extra chapter. Let’s start out with the idea that you define your parameters and your observable space; the latter is the expected input data.
There are two types of models in zfit:
functions, which are rather simple and “underdeveloped”; their usage is often not required.
PDF that are function which are normalized (over a specified range); this is the main model and is what we gonna use throughout the tutorials.
A PDF is defined by
where a and b define the normalization range (norm_range), over which (by inserting into the above definition) the integral of the PDF is unity.
zfit has a modular approach to things and this is also true for models. While the normalization itself (e.g. what are parameters, what is normalized data) will already be pre-defined in the model, models are composed of functions that are transparently called inside. For example, a Gaussian would usually be implemented by writing a Python function def gauss(x, mu, sigma), which does not care about the normalization and then be wrapped in a PDF, where the normalization and what is a parameter is defined.
In principle, we can go far by using simply functions (e.g. TensorFlowAnalysis/AmpliTF by Anton Poluektov uses this approach quite successfully for Amplitude Analysis), but this design has limitations for a more general fitting library such as zfit (or even TensorWaves, being built on top of AmpliTF). The main thing is to keep track of the different ordering of the data and parameters, especially the dependencies.
Let’s create a simple Gaussian PDF. We already defined the Space for the data before, now we only need the parameters. This are a different object than a Space.
Parameter¶
A Parameter (there are different kinds actually, more on that later) takes the following arguments as input:
Parameter(human readable name, initial value[, lower limit, upper limit]) where the limits are recommended but not mandatory. Furthermore, step_size can be given (which is useful to be around the given uncertainty, e.g. for large yields or small values it can help a lot to set this). Also, a floating argument is supported, indicating whether the parameter is allowed to float in the fit or not (just omitting the limits does not make a parameter constant).
Parameters have a unique name. This is served as the identifier for e.g. fit results. However, a parameter cannot be retrieved by its string identifier (its name) but the object itself should be used. In places where a parameter maps to something, the object itself is needed, not its name.
mu = zfit.Parameter('mu', 1, -3, 3, step_size=0.2)
sigma_num = zfit.Parameter('sigma42', 1, 0.1, 10, floating=False)
These attributes can be changed:
print(f"sigma is float: {sigma_num.floating}")
sigma_num.floating = True
print(f"sigma is float: {sigma_num.floating}")
sigma is float: False
sigma is float: True
PITFALL NOTEBOOKS: since the parameters have a unique name, a second parameter with the same name cannot be created; the behavior is undefined and therefore it raises an error. While this does not pose a problem in a normal Python script, it does in a Jupyter-like notebook, since it is an often practice to “rerun” a cell as an attempt to “reset” things. Bear in mind that this does not make sense, from a logic point of view. The parameter already exists. Best practice: write a small wrapper, do not rerun the parameter creation cell or simply rerun the notebook (restart kernel & run all). For further details, have a look at the discussion and arguments here
Now we have everything to create a Gaussian PDF:
gauss = zfit.pdf.Gauss(obs=obs, mu=mu, sigma=sigma_num)
Since this holds all the parameters and the observables are well defined, we can retrieve them
gauss.n_obs # dimensions
1
gauss.obs
('obs1',)
gauss.space
<zfit Space obs=('obs1',), axes=(0,), limits=(array([[-5.]]), array([[10.]]))>
gauss.norm_range
<zfit Space obs=('obs1',), axes=(0,), limits=(array([[-5.]]), array([[10.]]))>
As we’ve seen, the obs we defined is the space of Gauss: this acts as the default limits whenever needed (e.g. for sampling). gauss also has a norm_range, which equals by default as well to the obs given, however, we can explicitly change that with set_norm_range.
We can also access the parameters of the PDF in two ways, depending on our intention:
either by name (the parameterization name, e.g. mu and sigma, as defined in the Gauss), which is useful if we are interested in the parameter that describes the shape
gauss.params
OrderedDict([('mu', <zfit.Parameter 'mu' floating=True value=1>),
('sigma', <zfit.Parameter 'sigma42' floating=True value=1>)])
or to retrieve all the parameters that the PDF depends on. As this now may sounds trivial, we will see later that models can depend on other models (e.g. sums) and parameters on other parameters. There is one function that automatically retrieves all dependencies, get_params. It takes three arguments to filter:
floating: whether to filter only floating parameters, only non-floating or don’t discriminate
is_yield: if it is a yield, or not a yield, or both
extract_independent: whether to recursively collect all parameters. This, and the explanation for why independent, can be found later on in the
Simultaneoustutorial.
Usually, the default is exactly what we want if we look for all free parameters that this PDF depends on.
gauss.get_params()
OrderedSet([<zfit.Parameter 'mu' floating=True value=1>, <zfit.Parameter 'sigma42' floating=True value=1>])
The difference will also be clear if we e.g. use the same parameter twice:
gauss_only_mu = zfit.pdf.Gauss(obs=obs, mu=mu, sigma=mu)
print(f"params={gauss_only_mu.params}")
print(f"get_params={gauss_only_mu.get_params()}")
params=OrderedDict([('mu', <zfit.Parameter 'mu' floating=True value=1>), ('sigma', <zfit.Parameter 'mu' floating=True value=1>)])
get_params=OrderedSet([<zfit.Parameter 'mu' floating=True value=1>])
Functionality¶
PDFs provide a few useful methods. The main features of a zfit PDF are:
pdf: the normalized value of the PDF. It takes an argumentnorm_rangethat can be set toFalse, in which case we retrieve the unnormalized valueintegrate: given a certain range, the PDF is integrated. Aspdf, it takes anorm_rangeargument that integrates over the unnormalizedpdfif set toFalsesample: samples from the pdf and returns aDataobject
integral = gauss.integrate(limits=(-1, 3)) # corresponds to 2 sigma integral
integral
<tf.Tensor: shape=(1,), dtype=float64, numpy=array([0.95449974])>
Tensors¶
As we see, many zfit functions return Tensors. This is however no magical thing! If we’re outside of models, than we can always safely convert them to a numpy array by calling zfit.run(...) on it (or any structure containing potentially multiple Tensors). However, this may not even be required often! They can be added just like numpy arrays and interact well with Python and Numpy:
np.sqrt(integral)
array([0.97698502])
They also have shapes, dtypes, can be slices etc. So do not convert them except you need it. More on this can be seen in the talk later on about zfit and TensorFlow 2.0.
sample = gauss.sample(n=1000) # default space taken as limits
sample
<zfit.core.data.SampleData at 0x7f84b4f2e8b0>
sample.unstack_x()[:10]
<tf.Tensor: shape=(10,), dtype=float64, numpy=
array([ 1.2152566 , 2.81183774, 0.3578351 , 0.14692911, -0.46053768,
1.0086027 , 0.24786822, 0.79486641, -0.42387978, 0.31100973])>
sample.n_obs
1
sample.obs
('obs1',)
We see that sample returns also a zfit Data object with the same space as it was sampled in. This can directly be used e.g.
probs = gauss.pdf(sample)
probs[:10]
<tf.Tensor: shape=(10,), dtype=float64, numpy=
array([0.38980595, 0.07728027, 0.32461143, 0.27725891, 0.13730869,
0.39892752, 0.30065567, 0.39063626, 0.14476329, 0.31465064])>
NOTE: In case you want to do this repeatedly (e.g. for toy studies), there is a way more efficient way (see later on)
Plotting¶
so far, we have a dataset and a PDF. Before we go for fitting, we can make a plot. This functionality is not directly provided in zfit (but can be added to zfit-physics). It is however simple enough to do it:
def plot_model(model, data, scale=1, plot_data=True): # we will use scale later on
nbins = 50
lower, upper = data.data_range.limit1d
x = tf.linspace(lower, upper, num=1000) # np.linspace also works
y = model.pdf(x) * size_normal / nbins * data.data_range.area()
y *= scale
plt.plot(x, y)
data_plot = zfit.run(z.unstack_x(data)) # we could also use the `to_pandas` method
if plot_data:
plt.hist(data_plot, bins=nbins)
plot_model(gauss, data_normal)
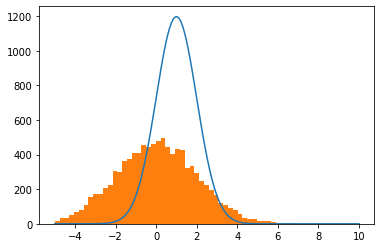
We can of course do better (and will see that later on, continuously improve the plots), but this is quite simple and gives us the full power of matplotlib.
Different models¶
zfit offers a selection of predefined models (and extends with models from zfit-physics that contain physics specific models such as ARGUS shaped models).
print(zfit.pdf.__all__)
['BasePDF', 'BaseFunctor', 'Exponential', 'CrystalBall', 'DoubleCB', 'Gauss', 'Uniform', 'TruncatedGauss', 'WrapDistribution', 'Cauchy', 'Poisson', 'Chebyshev', 'Legendre', 'Chebyshev2', 'Hermite', 'Laguerre', 'RecursivePolynomial', 'ProductPDF', 'SumPDF', 'GaussianKDE1DimV1', 'FFTConvPDFV1', 'ConditionalPDFV1', 'ZPDF', 'SimplePDF', 'SimpleFunctorPDF']
To create a more realistic model, we can build some components for a mass fit with a
signal component: CrystalBall
combinatorial background: Exponential
partial reconstructed background on the left: Kernel Density Estimation
mass_obs = zfit.Space('mass', (0, 1000))
# Signal component
mu_sig = zfit.Parameter('mu_sig', 400, 100, 600)
sigma_sig = zfit.Parameter('sigma_sig', 50, 1, 100)
alpha_sig = zfit.Parameter('alpha_sig', 200, 100, 400, floating=False) # won't be used in the fit
n_sig = zfit.Parameter('n sig', 4, 0.1, 30, floating=False)
signal = zfit.pdf.CrystalBall(obs=mass_obs, mu=mu_sig, sigma=sigma_sig, alpha=alpha_sig, n=n_sig)
# combinatorial background
lam = zfit.Parameter('lambda', -0.01, -0.05, -0.001)
comb_bkg = zfit.pdf.Exponential(lam, obs=mass_obs)
part_reco_data = np.random.normal(loc=200, scale=150, size=700)
part_reco_data = zfit.Data.from_numpy(obs=mass_obs, array=part_reco_data) # we don't need to do this but now we're sure it's inside the limits
part_reco = zfit.pdf.GaussianKDE1DimV1(obs=mass_obs, data=part_reco_data, bandwidth='adaptive')
Composing models¶
We can also compose multiple models together. Here we’ll stick to one dimensional models, the extension to multiple dimensions is explained in the “custom models tutorial”.
Here we will use a SumPDF. This takes pdfs and fractions. If we provide n pdfs and:
n - 1 fracs: the nth fraction will be 1 - sum(fracs)
n fracs: no normalization attempt is done by
SumPDf. If the fracs are not implicitly normalized, this can lead to bad fitting behavior if there is a degree of freedom too much
sig_frac = zfit.Parameter('sig_frac', 0.3, 0, 1)
comb_bkg_frac = zfit.Parameter('comb_bkg_frac', 0.25, 0, 1)
model = zfit.pdf.SumPDF([signal, comb_bkg, part_reco], [sig_frac, comb_bkg_frac])
In order to have a corresponding data sample, we can just create one. Since we want to fit to this dataset later on, we will create it with slightly different values. Therefore, we can use the ability of a parameter to be set temporarily to a certain value with
print(f"before: {sig_frac}")
with sig_frac.set_value(0.25):
print(f"new value: {sig_frac}")
print(f"after 'with': {sig_frac}")
before: <zfit.Parameter 'sig_frac' floating=True value=0.3>
new value: <zfit.Parameter 'sig_frac' floating=True value=0.25>
after 'with': <zfit.Parameter 'sig_frac' floating=True value=0.3>
While this is useful, it does not fully scale up. We can use the zfit.param.set_values helper therefore.
(Sidenote: instead of a list of values, we can also use a FitResult, the given parameters then take the value from the result)
with zfit.param.set_values([mu_sig, sigma_sig, sig_frac, comb_bkg_frac, lam], [370, 34, 0.18, 0.15, -0.006]):
data = model.sample(n=10000)
plot_model(model, data);
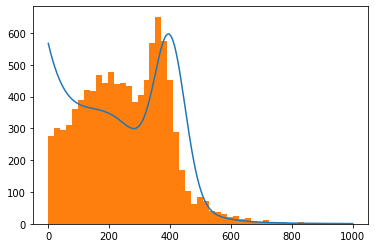
Plotting the components is not difficult now: we can either just plot the pdfs separately (as we still can access them) or in a generalized manner by accessing the pdfs attribute:
def plot_comp_model(model, data):
for mod, frac in zip(model.pdfs, model.params.values()):
plot_model(mod, data, scale=frac, plot_data=False)
plot_model(model, data)
plot_comp_model(model, data)
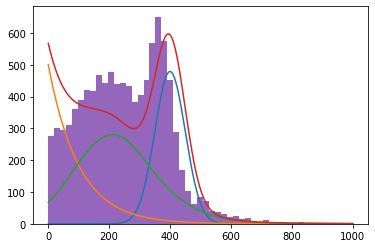
Now we can add legends etc. Btw, did you notice that actually, the frac params are zfit Parameters? But we just used them as if they were Python scalars and it works.
print(model.params)
OrderedDict([('frac_0', <zfit.Parameter 'sig_frac' floating=True value=0.3>), ('frac_1', <zfit.Parameter 'comb_bkg_frac' floating=True value=0.25>), ('frac_2', <zfit.ComposedParameter 'Composed_autoparam_2' params=OrderedDict([('param_0', <zfit.Parameter 'sig_frac' floating=True value=0.3>), ('param_1', <zfit.Parameter 'comb_bkg_frac' floating=True value=0.25>)]) value=0.45>)])
Extended PDFs¶
So far, we have only looked at normalized PDFs that do contain information about the shape but not about the absolute scale. We can make a PDF extended by adding a yield to it.
The behavior of the new, extended PDF does NOT change, any methods we called before will act the same. Only exception, some may require an argument less now. All the methods we used so far will return the same values. What changes is that the flag model.is_extended now returns True. Furthermore, we have now a few more methods that we can use which would have raised an error before:
get_yield: return the yield parameter (notice that the yield is not added to the shape parametersparams)ext_{pdf,integrate}: these methods return the same as the versions used before, however, multiplied by the yieldsampleis still the same, but does not require the argumentnanymore. By default, this will now equal to a poissonian sampled n around the yield.
The SumPDF now does not strictly need fracs anymore: if all input PDFs are extended, the sum will be as well and use the (normalized) yields as fracs
The preferred way to create an extended PDf is to use PDF.create_extended(yield). However, since this relies on copying the PDF (which may does not work for different reasons), there is also a set_yield(yield) method that sets the yield in-place. This won’t lead to ambiguities, as everything is supposed to work the same.
yield_model = zfit.Parameter('yield_model', 10000, 0, 20000, step_size=10)
model_ext = model.create_extended(yield_model)
alternatively, we can create the models as extended and sum them up
sig_yield = zfit.Parameter('sig_yield', 2000, 0, 10000, step_size=1)
sig_ext = signal.create_extended(sig_yield)
comb_bkg_yield = zfit.Parameter('comb_bkg_yield', 6000, 0, 10000, step_size=1)
comb_bkg_ext = comb_bkg.create_extended(comb_bkg_yield)
part_reco_yield = zfit.Parameter('part_reco_yield', 2000, 0, 10000, step_size=1)
part_reco.set_yield(part_reco_yield) # unfortunately, `create_extended` does not work here. But no problem, it won't change anyting.
part_reco_ext = part_reco
model_ext_sum = zfit.pdf.SumPDF([sig_ext, comb_bkg_ext, part_reco_ext])
Loss¶
A loss combines the model and the data, for example to build a likelihood. Furthermore, it can contain constraints, additions to the likelihood. Currently, if the Data has weights, these are automatically taken into account.
nll_gauss = zfit.loss.UnbinnedNLL(gauss, data_normal)
The loss has several attributes to be transparent to higher level libraries. We can calculate the value of it using value.
nll_gauss.value()
<tf.Tensor: shape=(), dtype=float64, numpy=999.9999999999966>
Notice that due to graph building, this will take significantly longer on the first run. Rerun the cell above and it will be way faster.
Furthermore, the loss also provides a possibility to calculate the gradients or, often used, the value and the gradients.
We can access the data and models (and possible constraints)
nll_gauss.model
[<zfit.<class 'zfit.models.dist_tfp.Gauss'> params=[mu, sigma42]]
nll_gauss.data
[<zfit.core.data.Data at 0x7f8544bce310>]
nll_gauss.constraints
[]
Similar to the models, we can also get the parameters via get_params.
nll_gauss.get_params()
OrderedSet([<zfit.Parameter 'mu' floating=True value=1>, <zfit.Parameter 'sigma42' floating=True value=1>])
Extended loss¶
More interestingly, we can now build a loss for our composite sum model using the sampled data. Since we created an extended model, we can now also create an extended likelihood, taking into account a Poisson term to match the yield to the number of events.
nll = zfit.loss.ExtendedUnbinnedNLL(model_ext_sum, data)
nll.get_params()
OrderedSet([<zfit.Parameter 'sig_yield' floating=True value=2000>, <zfit.Parameter 'comb_bkg_yield' floating=True value=6000>, <zfit.Parameter 'part_reco_yield' floating=True value=2000>, <zfit.Parameter 'mu_sig' floating=True value=400>, <zfit.Parameter 'sigma_sig' floating=True value=50>, <zfit.Parameter 'lambda' floating=True value=-0.01>])
Minimization¶
While a loss is interesting, we usually want to minimize it. Therefore we can use the minimizers in zfit, most notably Minuit, a wrapper around the iminuit minimizer.
The philosophy is to create a minimizer instance that is mostly stateless, e.g. does not remember the position (there are considerations to make it possible to have a state, in case you feel interested, contact us)
Given that iminuit provides us with a very reliable and stable minimizer, it is usually recommended to use this. Others are implemented as well and could easily be wrapped, however, the convergence is usually not as stable.
Minuit has a few options:
tolerance: the Estimated Distance to Minimum (EDM) criteria for convergence (default 1e-3)verbosity: between 0 and 10, 5 is normal, 7 is verbose, 10 is maximumgradient: if True, uses the Minuit numerical gradient instead of the TensorFlow gradient. This is usually more stable for smaller fits; furthermore the TensorFlow gradient can (experience based) sometimes be wrong.
minimizer = zfit.minimize.Minuit(gradient=True)
For the minimization, we can call minimize, which takes a
loss as we created above
optionally: the parameters to minimize
By default, minimize uses all the free floating parameters (obtained with get_params). We can also explicitly specify which ones to use by giving them (or better, objects that depend on them) to minimize; note however that non-floating parameters, even if given explicitly to minimize won ‘t be minimized.
Pre-fit parts of the PDF¶
Before we want to fit the whole PDF however, it can be useful to pre-fit it. A way can be to fix the combinatorial background by fitting the exponential to the right tail.
Therefore we create a new data object with an additional cut and furthermore, set the normalization range of the background pdf to the range we are interested in.
values = z.unstack_x(data)
obs_right_tail = zfit.Space('mass', (700, 1000))
data_tail = zfit.Data.from_tensor(obs=obs_right_tail, tensor=values)
with comb_bkg.set_norm_range(obs_right_tail):
nll_tail = zfit.loss.UnbinnedNLL(comb_bkg, data_tail)
minimizer.minimize(nll_tail)
Since we now fit the lambda parameter of the exponential, we can fix it.
lam.floating = False
lam
<zfit.Parameter 'lambda' floating=False value=-0.006958>
result = minimizer.minimize(nll)
plot_comp_model(model_ext_sum, data)
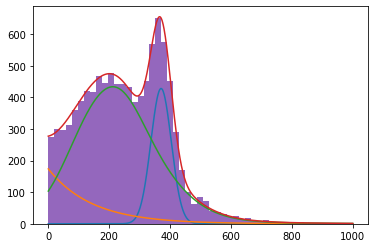
Fit result¶
The result of every minimization is stored in a FitResult. This is the last stage of the zfit workflow and serves as the interface to other libraries. Its main purpose is to store the values of the fit, to reference to the objects that have been used and to perform (simple) uncertainty estimation.
print(result)
FitResult
of
<ExtendedUnbinnedNLL model=[<zfit.<class 'zfit.models.functor.SumPDF'> params=[Composed_autoparam_5, Composed_autoparam_6, Composed_autoparam_7]] data=[<zfit.core.data.SampleData object at 0x7f84b4c94250>] constraints=[]>
with
<Minuit Minuit tol=0.001>
╒═════════╤═════════════╤══════════════════╤═════════╤═════════════╕
│ valid │ converged │ param at limit │ edm │ min value │
╞═════════╪═════════════╪══════════════════╪═════════╪═════════════╡
│
True
│ True
│ False
│ 0.00043 │ -1153 │
╘═════════╧═════════════╧══════════════════╧═════════╧═════════════╛
Parameters
name value at limit
--------------- ------- ----------
sig_yield 1796 False
comb_bkg_yield 1246 False
part_reco_yield 6955 False
mu_sig 370.6 False
sigma_sig 33.51 False
This gives an overview over the whole result. Often we’re mostly interested in the parameters and their values, which we can access with a params attribute.
print(result.params)
name value at limit
--------------- ------- ----------
sig_yield 1796 False
comb_bkg_yield 1246 False
part_reco_yield 6955 False
mu_sig 370.6 False
sigma_sig 33.51 False
This is a dict which stores any knowledge about the parameters and can be accessed by the parameter (object) itself:
result.params[mu_sig]
{'value': 370.567549184356}
‘value’ is the value at the minimum. To obtain other information about the minimization process, result contains more attributes:
fmin: the function minimum
edm: estimated distance to minimum
info: contains a lot of information, especially the original information returned by a specific minimizer
converged: if the fit converged
result.fmin
-1152.6348581767088
Estimating uncertainties¶
The FitResult has mainly two methods to estimate the uncertainty:
a profile likelihood method (like MINOS)
Hessian approximation of the likelihood (like HESSE)
When using Minuit, this uses (currently) it’s own implementation. However, zfit has its own implementation, which are likely to become the standard and can be invoked by changing the method name.
Hesse is also on the way to implement the corrections for weights.
We can explicitly specify which parameters to calculate, by default it does for all.
result.hesse(method='minuit_hesse')
{<zfit.Parameter 'sig_yield' floating=True value=1796>: {'error': 70.29135548741861,
'cl': 0.68268949},
<zfit.Parameter 'comb_bkg_yield' floating=True value=1246>: {'error': 92.21120729864366,
'cl': 0.68268949},
<zfit.Parameter 'part_reco_yield' floating=True value=6955>: {'error': 143.12177069495814,
'cl': 0.68268949},
<zfit.Parameter 'mu_sig' floating=True value=370.6>: {'error': 1.3680686008193916,
'cl': 0.68268949},
<zfit.Parameter 'sigma_sig' floating=True value=33.51>: {'error': 1.2438922675171318,
'cl': 0.68268949}}
# result.hesse(method='hesse_np')
We get the result directly returned. This is also added to result.params for each parameter and is nicely displayed with an added column
print(result.params)
name value minuit_hesse at limit
--------------- ------- -------------- ----------
sig_yield 1796 +/- 70 False
comb_bkg_yield 1246 +/- 92 False
part_reco_yield 6955 +/- 1.4e+02 False
mu_sig 370.6 +/- 1.4 False
sigma_sig 33.51 +/- 1.2 False
errors, new_result = result.errors(params=[sig_yield, part_reco_yield, mu_sig]) # just using three for speed reasons
# errors, new_result = result.errors(params=[yield_model, sig_frac, mu_sig], method='zfit_error')
print(errors)
OrderedDict([(<zfit.Parameter 'sig_yield' floating=True value=1796>, {'lower': -69.04045217754343, 'upper': 71.64844344330136, 'is_valid': True, 'upper_valid': True, 'lower_valid': True, 'at_lower_limit': False, 'at_upper_limit': False, 'nfcn': 76, 'original': <MError number=0 name='sig_yield' lower=-69.04045217754343 upper=71.64844344330136 is_valid=True lower_valid=True upper_valid=True at_lower_limit=False at_upper_limit=False at_lower_max_fcn=False at_upper_max_fcn=False lower_new_min=False upper_new_min=False nfcn=76 min=1796.4520016779795>, 'cl': 0.68268949}), (<zfit.Parameter 'part_reco_yield' floating=True value=6955>, {'lower': -142.44713996257306, 'upper': 144.0324814110507, 'is_valid': True, 'upper_valid': True, 'lower_valid': True, 'at_lower_limit': False, 'at_upper_limit': False, 'nfcn': 54, 'original': <MError number=2 name='part_reco_yield' lower=-142.44713996257306 upper=144.0324814110507 is_valid=True lower_valid=True upper_valid=True at_lower_limit=False at_upper_limit=False at_lower_max_fcn=False at_upper_max_fcn=False lower_new_min=False upper_new_min=False nfcn=54 min=6954.577183771976>, 'cl': 0.68268949}), (<zfit.Parameter 'mu_sig' floating=True value=370.6>, {'lower': -1.3720748780003589, 'upper': 1.3658734319899464, 'is_valid': True, 'upper_valid': True, 'lower_valid': True, 'at_lower_limit': False, 'at_upper_limit': False, 'nfcn': 40, 'original': <MError number=3 name='mu_sig' lower=-1.3720748780003589 upper=1.3658734319899464 is_valid=True lower_valid=True upper_valid=True at_lower_limit=False at_upper_limit=False at_lower_max_fcn=False at_upper_max_fcn=False lower_new_min=False upper_new_min=False nfcn=40 min=370.567549184356>, 'cl': 0.68268949})])
print(result.params)
name value minuit_hesse minuit_minos at limit
--------------- ------- -------------- ------------------- ----------
sig_yield 1796 +/- 70 - 69 + 72 False
comb_bkg_yield 1246 +/- 92 False
part_reco_yield 6955 +/- 1.4e+02 -1.4e+02 +1.4e+02 False
mu_sig 370.6 +/- 1.4 - 1.4 + 1.4 False
sigma_sig 33.51 +/- 1.2 False
What is ‘new_result’?¶
When profiling a likelihood, such as done in the algorithm used in errors, a new minimum can be found. If this is the case, this new minimum will be returned, otherwise new_result is None. Furthermore, the current result would be rendered invalid by setting the flag valid to False. Note: this behavior only applies to the zfit internal error estimator.
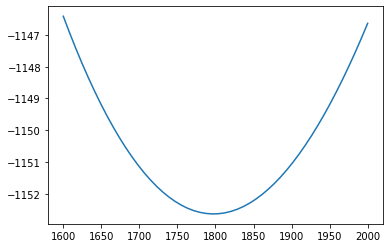
A simple profile¶
There is no default function (yet) for simple profiling plot. However, again, we’re in Python and it’s simple enough to do that for a parameter. Let’s do it for sig_yield
x = np.linspace(1600, 2000, num=50)
y = []
sig_yield.floating = False
for val in x:
sig_yield.set_value(val)
y.append(nll.value())
sig_yield.floating = True
zfit.param.set_values(nll.get_params(), result)
<zfit.util.temporary.TemporarilySet at 0x7f84b44123d0>
plt.plot(x, y)
[<matplotlib.lines.Line2D at 0x7f84b424d640>]
We can also access the covariance matrix of the parameters
result.covariance()
array([[ 4.94087470e+03, 1.56826981e+03, -4.71184853e+03,
-2.33547729e+01, 4.04122787e+01],
[ 1.56826981e+03, 8.50290683e+03, -8.82309054e+03,
-1.22626416e+01, 1.97178802e+01],
[-4.71184853e+03, -8.82309054e+03, 2.04838414e+04,
3.56080789e+01, -6.01145373e+01],
[-2.33547729e+01, -1.22626416e+01, 3.56080789e+01,
1.87161171e+00, -4.34076667e-01],
[ 4.04122787e+01, 1.97178802e+01, -6.01145373e+01,
-4.34076667e-01, 1.54726799e+00]])
End of zfit¶
This is where zfit finishes and other libraries take over.
Beginning of hepstats¶
hepstats is a library containing statistical tools and utilities for high energy physics. In particular you do statistical inferences using the models and likelhoods function constructed in zfit.
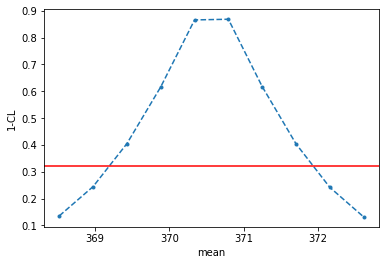
Short example: let’s compute for instance a confidence interval at 68 % confidence level on the mean of the gaussian defined above.
from hepstats.hypotests import ConfidenceInterval
from hepstats.hypotests.calculators import AsymptoticCalculator
from hepstats.hypotests.parameters import POIarray
calculator = AsymptoticCalculator(input=result, minimizer=minimizer)
value = result.params[mu_sig]["value"]
error = result.params[mu_sig]["minuit_hesse"]["error"]
mean_scan = POIarray(mu_sig, np.linspace(value - 1.5*error, value + 1.5*error, 10))
ci = ConfidenceInterval(calculator, mean_scan)
ci.interval()
Confidence interval on mu_sig:
369.1996462470642 < mu_sig < 371.929713802475 at 68.0% C.L.
{'observed': 370.567549184356,
'upper': 371.929713802475,
'lower': 369.1996462470642}
from utils import one_minus_cl_plot
ax = one_minus_cl_plot(ci)
ax.set_xlabel("mean")
Text(0.5, 0, 'mean')
There will be more of hepstats later.